Look, you can’t complain about this after giving us so many scenarios involving N locked chests and M unlabeled keys.
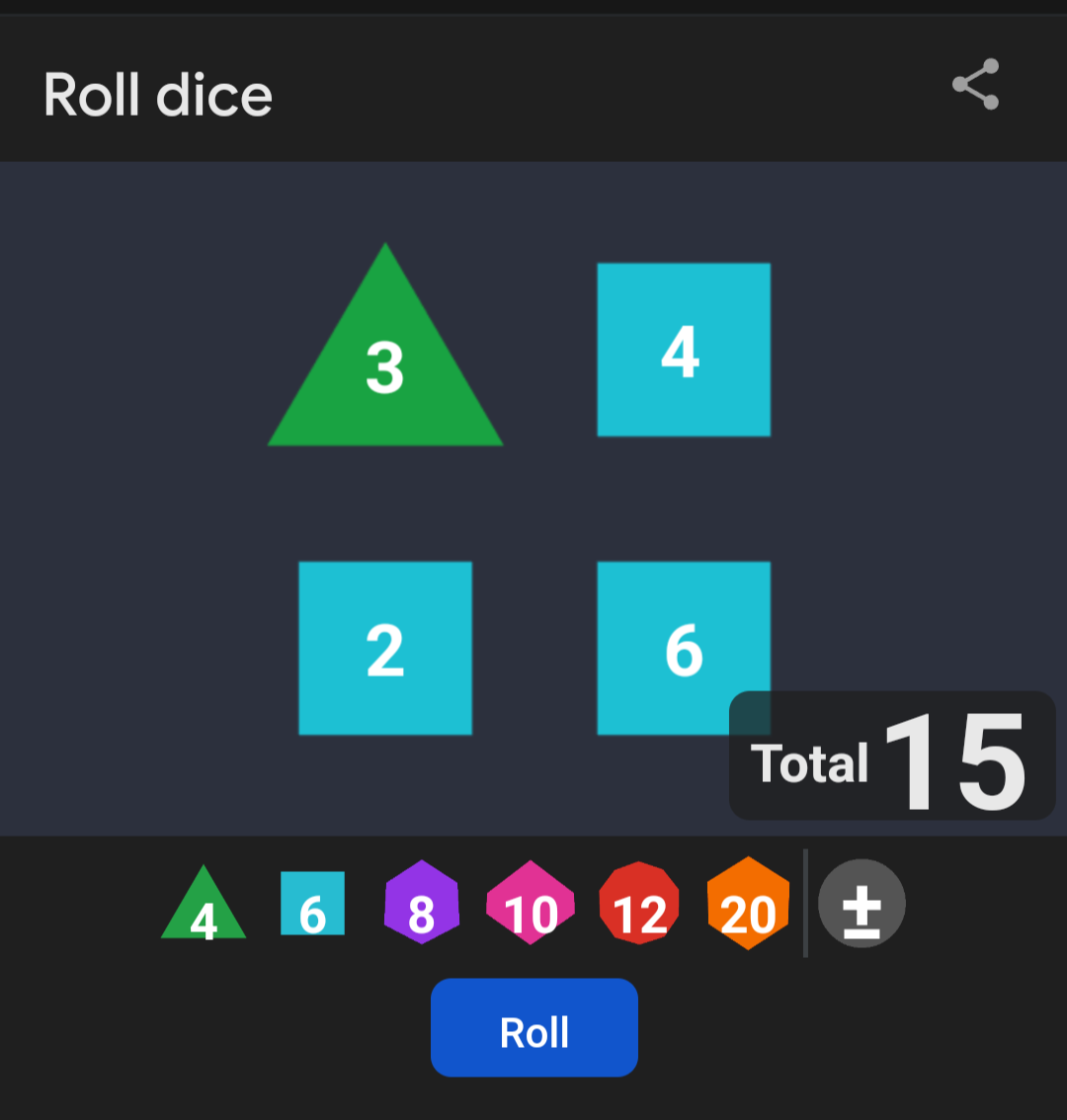
I rolled 15. 😭
The second you let fly the arrow, you feel the burning in your fingers. The world around you fades as you look down in horror at the crimson thorns that dance on the surface of your hand. You hardly notice that the arrow met its mark - the goblin falls to the ground, pierced deep through its eye - as you, too, fall to your knees. You bellow in pain, the howling echoing through the cavern as the magical vine constricts, the thorns piercing into your flesh.
Roll for wisdom.
Amazing. Ok, and…well at least I’m consistent? 3-1.
You fail the saving throw. The curse takes hold of you, the Bane of Thorny Improbability, which damns its bearer to be eternally plagued by probability and combinatorics conundra in their adventures.
You know that you possess an antidote to stave off the worst effects of the curse, but you have three unlabeled flasks at your belt, all of which have an equal probability of being the cure. You choose a flask at random, but as you seek to dislodge it, one of the other flasks falls to the earth and shatters. The liquid eats through the rock of the cavern, giving off acrid smoke, and you recognize that the fallen vial was a deadly poison, not the cure.
Knowing that the second flask did not contain the cure, do you have a better chance of salvation by drinking the flask you originally chose, or switching to the remaining unfallen flask?
Monty-hall, I’m switching boss.
I agree with the Cuban Dance. I’d switch the choice.
Aside, do you DM? I love how you’ve written the above.
I used to DM quite a bit, though I’ve been a player in my last two campaigns! But I also like watching things like D20 and I read a fair bit of fantasy as well.
I have never played R&D (or, I did once, but had a bad experience), so bear with me.
Is it ever allowed to simply do the thing, instead of rolling dice? For example is this case, for example place 5+5 tokens upside down, and pick two of them? Or fold pieces of paper, etc?
You play the game with humans, you are “allowed” to do what ever you want and doesn’t annoy the others. I like your idea with the tokens.
Absolutely!
The rules are a base framework for the DM to build upon.
Also the scenario in the comic isn’t actual DnD it’s really a math problem phrased in a DnD setting using standard DnD dice. In a real game the DM would probably do something like what you described.
I’d absolutely allow something like that at my table. Something like this isn’t going to have explicit rules, so even in a serious RAW (Rules As Written) game, the GM is going to have to come up with something. It’s just that we all have dice and may not have the right setup for tokens, etc.
Really, the simple way to do it is have arrows #1-5 be the cursed ones. The player then rolls a D10 to see which ones are pulled, rerolling on repeat “arrows”.
You have less arrows to pull from on subsequent rolls. You can’t keep using a D10.
That’s why you reroll on already taken numbers. Or drop down a die size every two arrows.
Now someone has to do the math on how many rolls on average it will take to resolve the action given the chance of rerolls.
The dm can make up whatever rules they want! That’s the great thing about it. I’ve never heard of anyone doing that, but in this case it sounds like a great idea to simplify the whole thing.
Edit: that’s also the terrible thing about it and if you have a bad DM they can make you miserable. That could be why you had a bad experience?
Dices are only used if there is a fail condition.
Folding a paper doesn’t have one.
Folding an crane for an origami competition does.
For the probability that at least one arrow picked is cursed: 1/2 + 1/2 × 5/9 = 14/18 = 7/9. (The probability that you picked it the first time, plus the probability that you missed it the first time but picked it the second time).
a dice probability calculator tells me probability of 3d6 + 1d4 at least 16 is 2/9. So the DM is correct.
- Sidenote: it doesn’t matter whether you grab the arrows one at a time or with both hands at the same time. Unless your party is trying to figure out which arms to amputate.
The math is easier if you look for the probability that the arrows are safe. If you do it that way, it’s simply 1/2*4/9, or 2/9.
That is true. Cueball had asked the question in the way I described, but the check was done in the inverse which is easier to do the math on.
Xkcd is smart, so I’m likely missing something.
But a random 2 out of 10, just roll two d10s and call it a day.
2d10 would be used if each arrow had a 10% chance of being cursed. But that’s not the case. There are 10 arrows, five are cursed, and 2 are selected. Therefore the first arrow would have a 5/10 chance of being cursed, while the second selection would have either a 4/9 or 5/9 chance of being cursed depending on whether or not the first arrow was cursed.
To solve this, requires using combinatorics. There are 10 choose 2 (45) ways to choose two arrows, of which there are 5 choose 2 (10) ways to choose 2 arrows that are non-cursed. This works out to be 2/9 odds to pull two safe arrows. Which means you need to get funkier with the dice.
Therefore the first arrow would have a 5/10 chance of being cursed, while the second selection would have either a 4/9 or 5/9 chance of being cursed depending on whether or not the first arrow was cursed.
If they pulled one, checked if it was cursed, and then pulled another, you’d be right
But they pulled two out of ten at the same time.
So roll two d10s, and say odds are cursed and even would regular. And that’s good enough.
I mean, maybe I’m missing something and I didn’t spell it out exactly what I meant in the first comment, but that should be the exact same odds as the action.
But what if I roll 2 times 1? I can’t pull arrow 1 twice!
Specific number doesn’t matter.
We have a binary result: cursed or regular. You probably wouldn’t lose anything by flipping a coin twice as long as the distribution of the arrows in the quiver is truly random.
Like, if you’re looking closer than that, you might as well account for when the arrows were added to the quiver, if they were added at the same time, how much the quiver has been jostled. The line has to be drawn somewhere, which I think is literally the joke of the comic…
There’s a very very simple solution but the DM is about to overthink and come up with the same result as the easy way, which they’ll realize after taking the long way around.
I know I’ve lost a lot of time by thinking “it’s worth being exact” and then I found out, no it really wasn’t worth it.
you will lose. the first arrow has 50% of being cursed the second 4/9 or 5/9.
That is if he pulled two individually, one after another.
Not two at the same time.
The odds are two out of ten.
There is no simpler way to explain this, I’m sorry if it still isn’t working
the odds of what exactly are 2/10?
Re-roll on a repeat
This is where a LLM might come in handy. Just tell it the parameters and say roll random. I think D&D could really benefit from the LLM. Shouldn’t be too hard to just let it be the DM. That way everyone can be in the party 😂
Except an LLM has no way to roll anything random, it will just predict the most likely text for a random roll, which isn’t remotely the same thing.
Why couldn’t they be paired with a true rng? They can reference outside sources.
Why use dice and simple math to solve a problem, when we can use an enormous pile of circuitry, electricity and vector calculus to get an algorithmically determined string of text that contains a probabilistically likely description of the correct dice to roll?
You have a 1 in 2 chance of pulling a cursed arrow the first time.
If you pulled a cursed arrow the first time, the second arrow has a 4 in 9 chance to be cursed. Otherwise, it’s 5 in 9.
Personally I’d have resolved this as a single d10 once, and rerolled a 10 on the second arrow. I haven’t done the math to know if 3d6+1d4 <16 yields the same probability though.
I dm Call of Cthulhu, so simply roll a luck check.
The chance doesn’t follow maths, it follows the whims of That Which We Do Not See.
And Randall has pushed his luck with them too far already.I was gonna say, sounds like a great use-case for quantum statistics. Until the roll, each arrow is in a superposition where it can be said to be simultaneously cursed and normal. Luck check for each shot until all of either are fully gone.
Yeah, d10 (1-5 cursed, 6-10 normal), then repeat with 1 or 10 being a reroll. I’m curious what the intent of the character was, whether they’re looking for a simple answer or something contrived like the DM’s answer.
then repeat with 1 or 10 being a reroll
or: repeat with the already rolled number being a reroll
Its xkcd so I assume Randall et al did the math.
From a play session perspective? If the GM is that good that they can mental math it, I would much rather be given one roll than a series of rolls. Ask anyone about their horror stories about grappling in 3e about how much that kills the game flow.
Also: The verbiage is ambiguous (less so if you have the context of how many attacks per round a player has and what feat they are using) but I think you can represent “I grabbed two at once” and “I grabbed one and then one” with a binomial coefficient. Been more than a minute but poking chatgpt to remember the notation (nCk) and it is likely representable as (5C2)/(10C2) which is approximately 22.2%.
As for the dice? I forget if the type of die meaningfully impacts this but 3d6+1d4=4-22. Whether a 16 maps to that 22.2% range is beyond my brain right now as this comment was mostly because I forgot the difference between nCk and nPk and felt like googling that.
The type of dice used can meaningfully impact this. The chance of a 2 or 12 rolling 2d6 is 1/36, the chance rolling 1d8+1d4 is 1/32. The chance of rolling 7 on 2d6, the most common result, is 1/6. The chance of rolling a 5, 6, 7, 8, or 9 on a 1d8+1d4, all equally likely, is 1/8 each.
Unlike you I can’t begin to remember the elegant way to find this. I also assume Randall would have it at least close to right.
Anydice.com can handle this stuff easily. As already pointed out in another comment, it does perfectly match. What it will not tell you is if you grabbed one or 2 arrows, though presumably a roll of 1-x could be used to say you got one, and x+1-15 means you got two.
Everyone out here using a dice calculator, but can someone answer
- Given a value x in (0,1) is there a set of dice and AC such that sum(roll{n_iDv_i}) > AC has probability x?
- Is there a sequence of finite set of dice and sequence of some AC for which we can get arbitrarily close to any probability?
irrational numbers will always be out of reach for a finite set of dice. I think if you restrict the set to the rationals, you will still run into trouble because there’s a finite number of dice and an infinite number of primes, so there will always be a big enough prime whose value you will be unable to get on the denominator. E.g. if you restrict to only a d2 and d3, you can’t get a denominator of 5 for your probability. So add a d5. Now you can’t get a denominator of 7, and so forth.
But all the primes would suffice especially as you’ve excluded 1 in the set. Otherwise, include a D1 and you’re golden.
To be extra clear, if you have an infinite set of dice, one for each prime, then you can attain a given probability using a finite subset of those dice. If you allow for the use of infinite dice and infinite rolls, my intuition says you can get the whole interval but let’s think about it.
It’s true that every real can be expressed as a convergent sequence of rationals, and that between any two real numbers there is at least one rational number. You can use this to construct a sequence of rationals that approaches the real numbers we want in the interval, and because we have all the prime dice and I have (not rigorously) proved this is enough to get any rational, we can roll any probability in our sequence. So we can get as close as we like to the real number.





